::DIE::

Concepto de señal

Señal

Es una variable física que contiene información sobre la naturaleza, el comportamiento de algún fenómeno físico o un proceso creado por el ser humano.

Las señales pueden representarse mediante una función de una o más variables, y se procesan y transforman a través de sistemas.

Sistema

Es el proceso que transforma señales.

Señal de Entrada
Excitación

Sistema

Señal de Salida
Respuesta

Clasificación de las señales

Las señales se clasifican en diferentes formas, una de ellas es la siguiente:

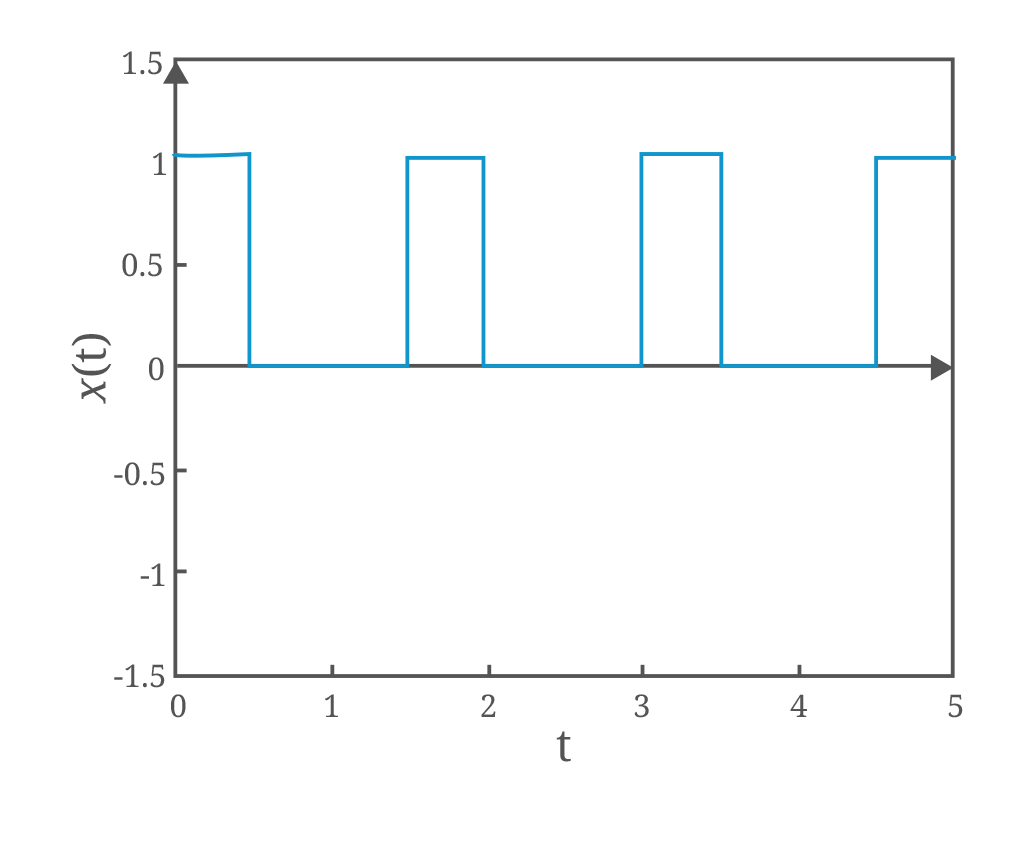
Tiempo continuo x(t)
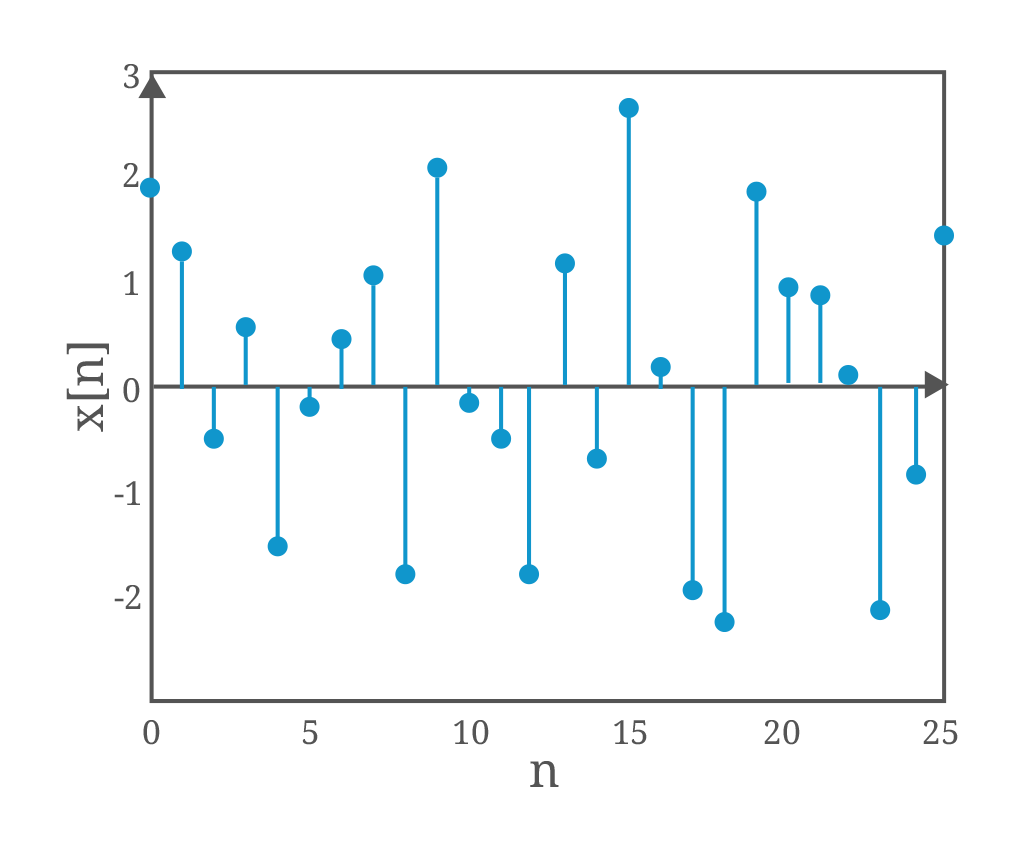
Tiempo discreto x[n]

{

Determinísticas y aleatorias
Periódicas y aperiódicas
Energía y de potencia

Ejemplos de señales de valor continuo y valor discreto

Señales de valor continuo

Señal de TC de valor continuo

Señal de TD de valor continuo

Señales de valor discreto

Señal de TC de valor discreto (señal digital)

Señal de TD de valor discreto

Características de las señales

Temperatura ambiental

Sonido de la tecla Do4 de un Piano

Espectro de la nota Do4 de un Piano

Imagen de una superficie

Algunas señales reales del mundo

Número de personas que entran a un Centro Comercial

Gráfica de control de calidad del largo de Placas de Metal

Incremento de la Población Mundial
(1750-2010)

¿Sabías que…?

Las señales de TD también se obtienen al muestrear señales de TC.
El muestreo significa la adquisición de valores de una señal de TC en puntos discretos en el tiempo.

Señales determinísticas y aleatorias

Señal con discontinuidades

Señal aleatoria de TC de valor continuo (ruido)

Señal aleatoria de TD de valor continuo

Señal digital

g(t) Señal de TC determinística

Señal de DT determinística

Señales periódicas y aperiódicas

Son señales periódicas si cumplen:

Si no se cumplen, son señales aperiódicas.

Señales periódicas

Señales aperiódicas

Éstas son las funciones singulares de TC:

Impulso unitario
Escalón unitario
Rampa unitaria
Doblete unitario

Funciones singulares de TC

Las funciones generalizadas de las funciones singulares se denotan como u_i-1 (t) y u_i+1 (t), y están relacionadas mediante integrales y derivadas.

Funciones singulares relacionadas con integrales

Es una función ideal que presenta las siguientes características:

Duración cero
Amplitud infinita
Área unitaria

Considerando i = 0 en la función u_i-1 (t):

Considerando i = -1 en la función u_i-1 (t):

De la misma forma, continúa la generación de funciones de mayor orden al considerar otros valores de i en la función u_i-1 (t).

Funciones singulares relacionadas con derivadas

Considerando ahora la función u_i+1 (t) derivada:

u_i+1(t) =
d u_i (t) / d t
Partiendo de la función “rampa”, tomando i = -2, se obtiene la derivada de la rampa que es precisamente el escalón unitario u_-1 (t):
La derivada de escalón i = -1 es:

u₀(t) =
d u_-1 (t) / d t

Se pensaría que es cero para todo t. Sin embargo, si en la discontinuidad, t=0, se considera una variación lineal en un intervalo infinitesimal comprendido en |a/2|, entonces la derivada en ese intervalo corresponde a una aproximación al impulso δ_α (t), donde en el límite lim ⁡α → 0, la derivada corresponde al impulso δ(t).

Función seno cardinal sinc(t)

Tiene una singularidad en t = 0 que se define con una amplitud de 1.

Función unitaria
Su área y amplitud es 1

∞ ∫ -∞

sinc(t)dt=1

Normalizada:

sinc(t)=

sen(πt) / πt

No normalizada:

Sa(t)=

sen(t) / t

∞ ∫ -∞

sa(t)dt=π

Función exponencial generalizada de base e

x(t)=Ce ^at

x(t) es una función real si C y a son reales:

C es constante y a > 0

C constante y a < 0

C constante y a = 0

Función exponencial compleja

x(t)=Ce ^at

x(t) es una función compleja si:

C es constante y a=jω₀.

x(t)= Ce^jω₀t

(a) Parte real de f(t)

(b) Parte Imag. f(t)

Y mediante la relación de Euler:

Ce^j(ω₀t) = C cos(ω₀t) + jCsen(ω₀t)

La cual se puede graficar de dos formas:

La parte real y la parte imaginaria (a) y (b).

La magnitud y el ángulo (c) y (d).

(d) Ángulo de f(t)

De manera adicional, si:

C= C₁e^jθ y a= jω₀

C1e^j(ω₀t+θ)=C₁cos(ω₀t +θ)+ jC₁sen(ω₀t+θ)

De tal forma que:

C₁cos(ω₀t+θ)= C₁Re{e^j(ω₀t+θ)}

C₁sen(ω₀t+θ)=C₁Img{e^j(ω₀t+θ)}

Se destaca que todas las exponenciales complejas de tiempo continuo son periódicas:

x(t)=Ce ^at

Considerando:

C=C₁e^jθ y a=r+jω₀

(a) Exp compleja decreciente r<0
Sustituyendo:

x(t)=C₁e^rt e^j(ω₀t+θ)

(b) Exp compleja creciente r>0
Mediante la relación de Euler, se obtiene:

x(t)=C₁e^rt(cos(ω₀t +θ)+j sem(ω₀t+θ))

(c) Exp compleja r=0